
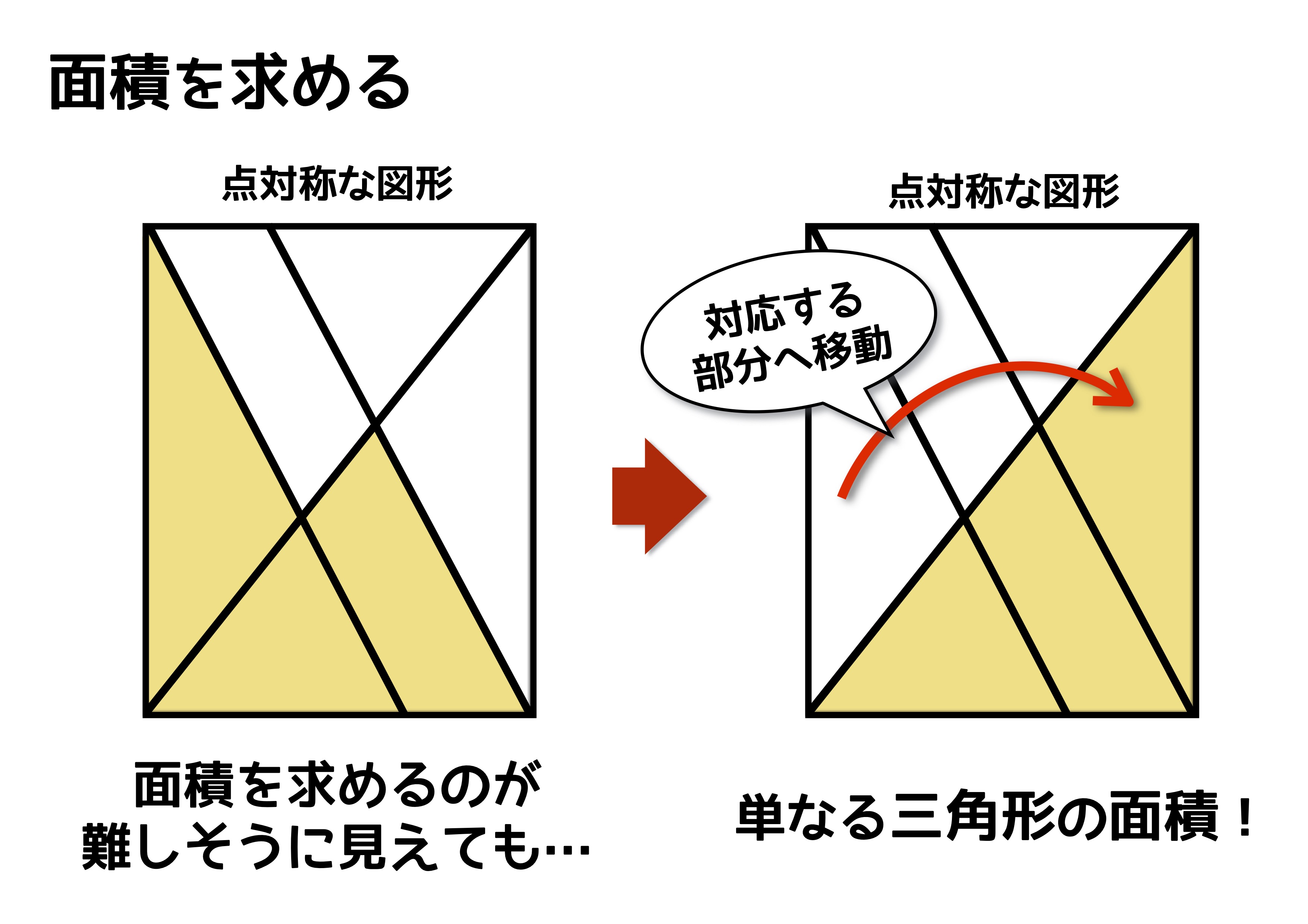
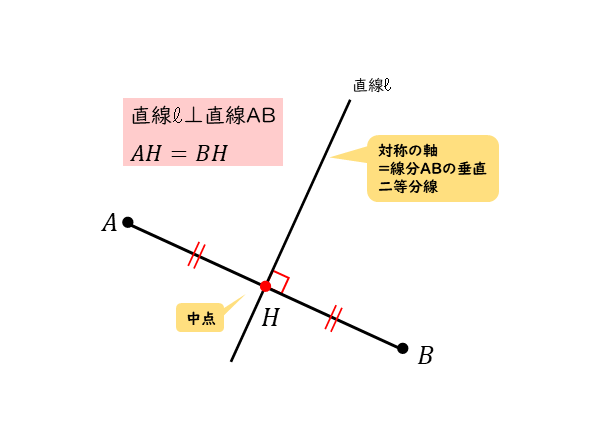
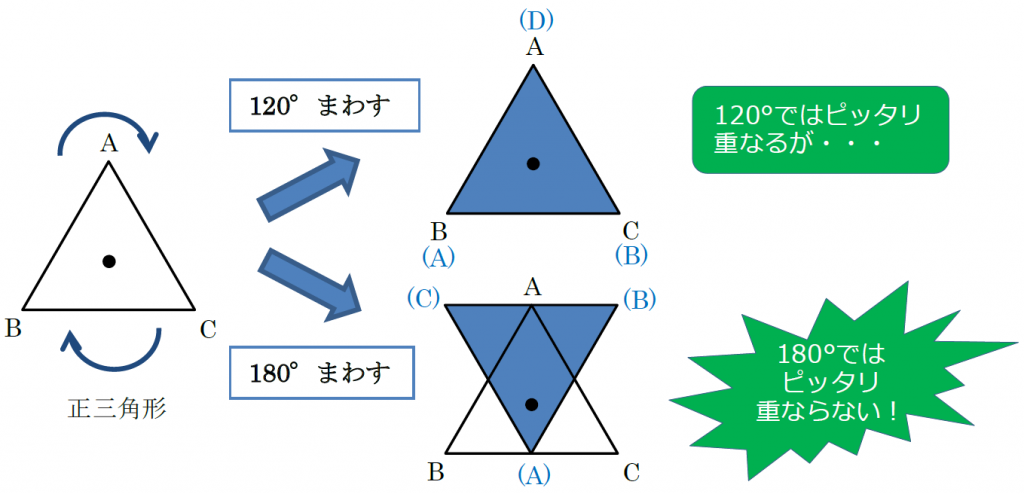
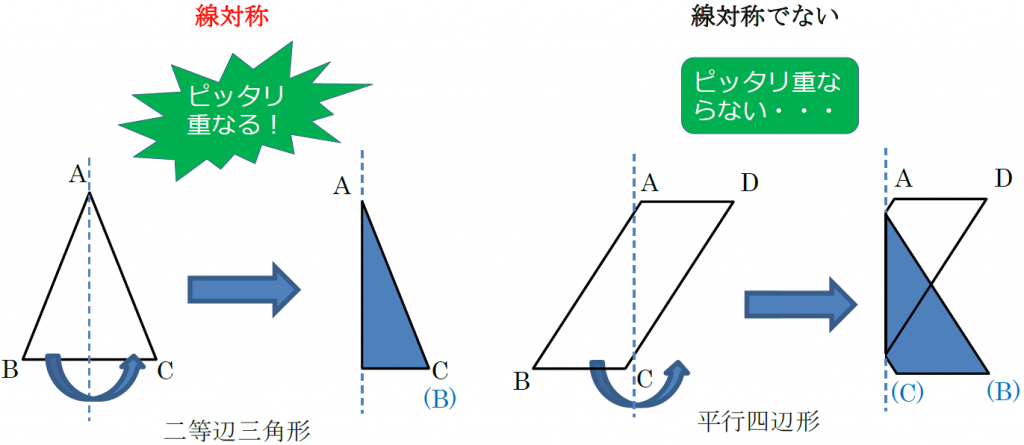
図形の対称移動の作図手順と性質 数学fun
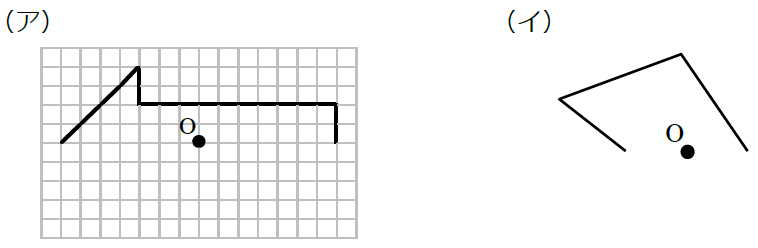
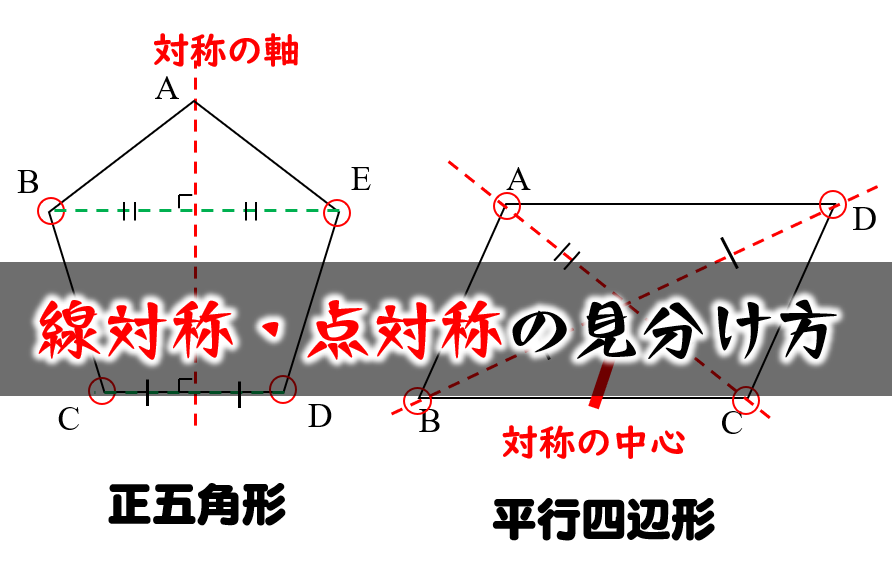
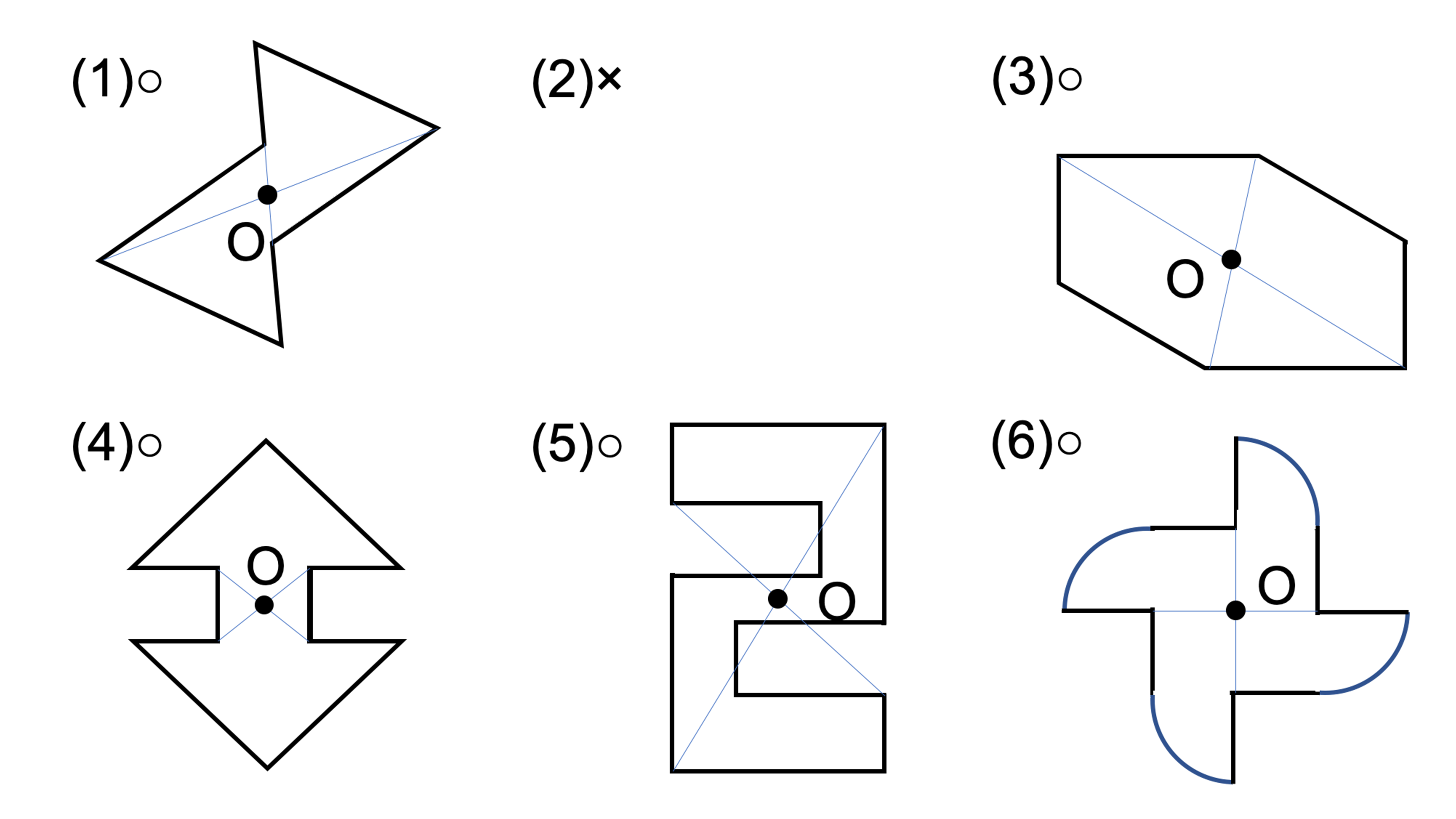
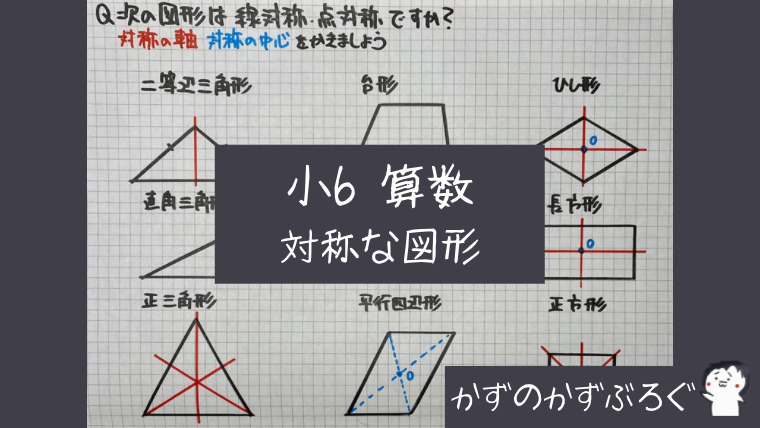
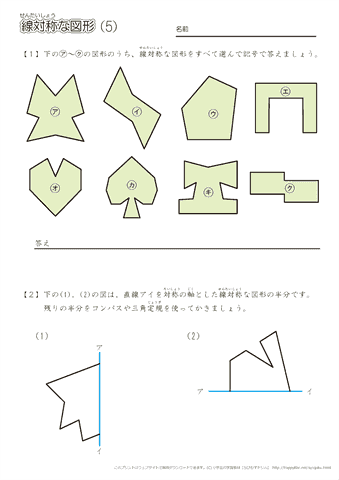
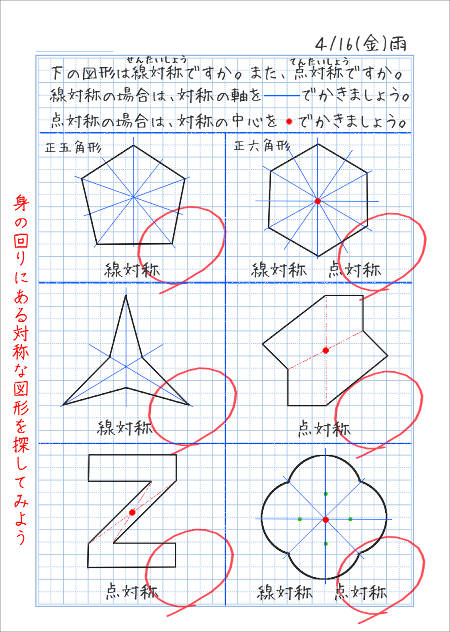
jis 対称度とは、データム軸直線またはデータム中心平面に関してたがいに対称であるべき形体の対象位置からの狂いの大きさである。 対称度の普通公差 (jis b 0419 1991) 対称度の普通公差は下記のとおりである。このとき、対称となるふたつの辺のうち、長いほうをデータムとする。線対称と点対称 軸の数は6本 正七角形 線対称 軸の数は7本 正八角形 線対称と点対称 軸の数は8本 線対称と点対称の調べ方と、軸の数の見つけ方は、これからもよく使うので覚えましょう。 練習問題 下のマークは、いろいろな自動車会社のマークです。
点 対称 書き方
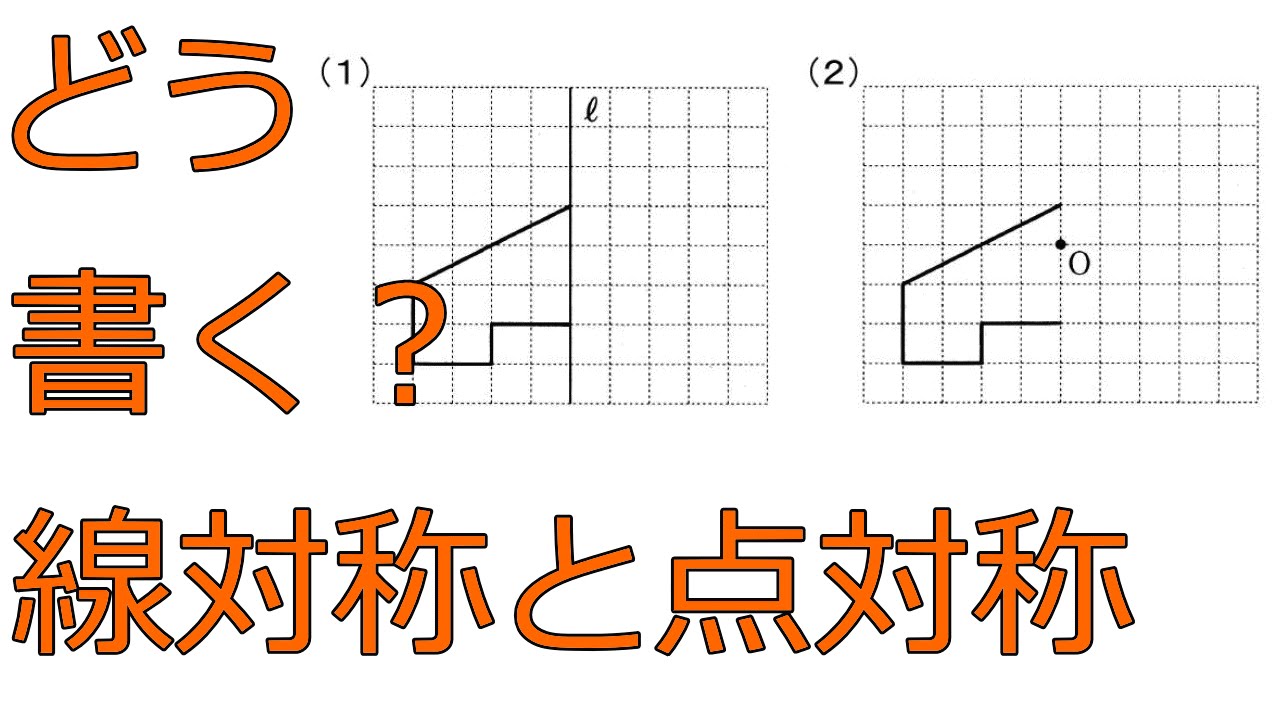
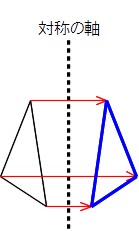
点 対称 書き方- 解決の鍵は「点対称」のほうにあった。 「点対称」の別称で「二回対称」という呼び方があることがわかった。 180度回転を2回繰り返したら図形がもとの位置に戻ってくるからだろう。 ならば、図形を90度ずつ回転させて毎回重なるとき、 その図形は「4 悩みのタネは、「線対称」と「点対称」に由来している、と思う。 それぞれ、私の教育課程では中学初期に現れた。 ある線を基準に図形を分けたとき、双方の図形が一致する性質。 鏡像対称ともいう。 ある点を基準に図形を回転させたとき、回転前の
線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun
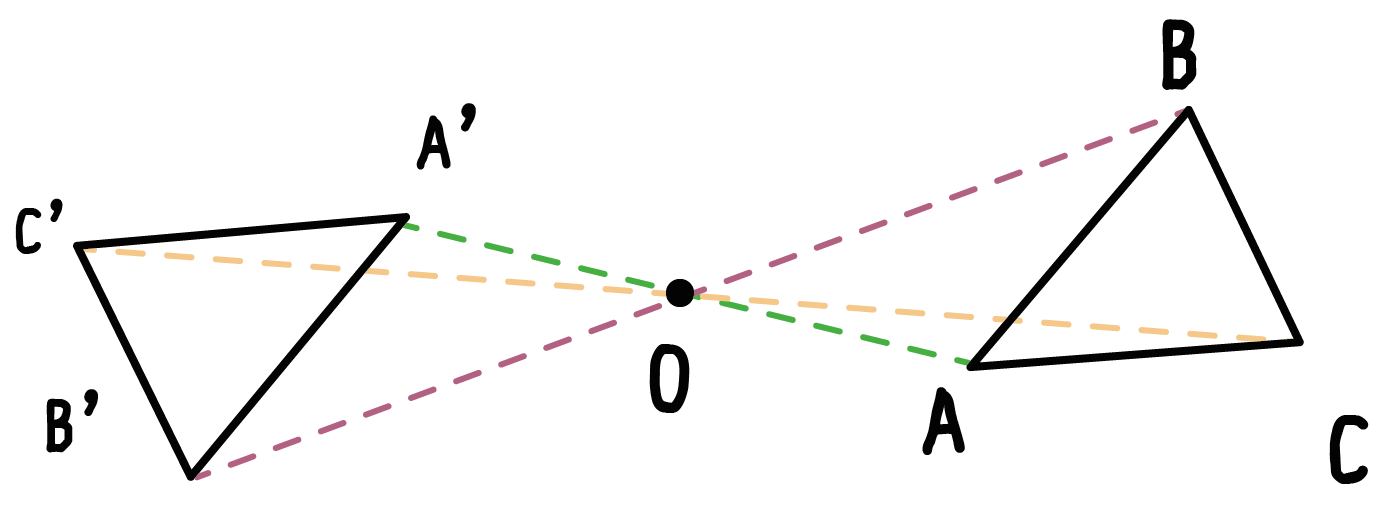
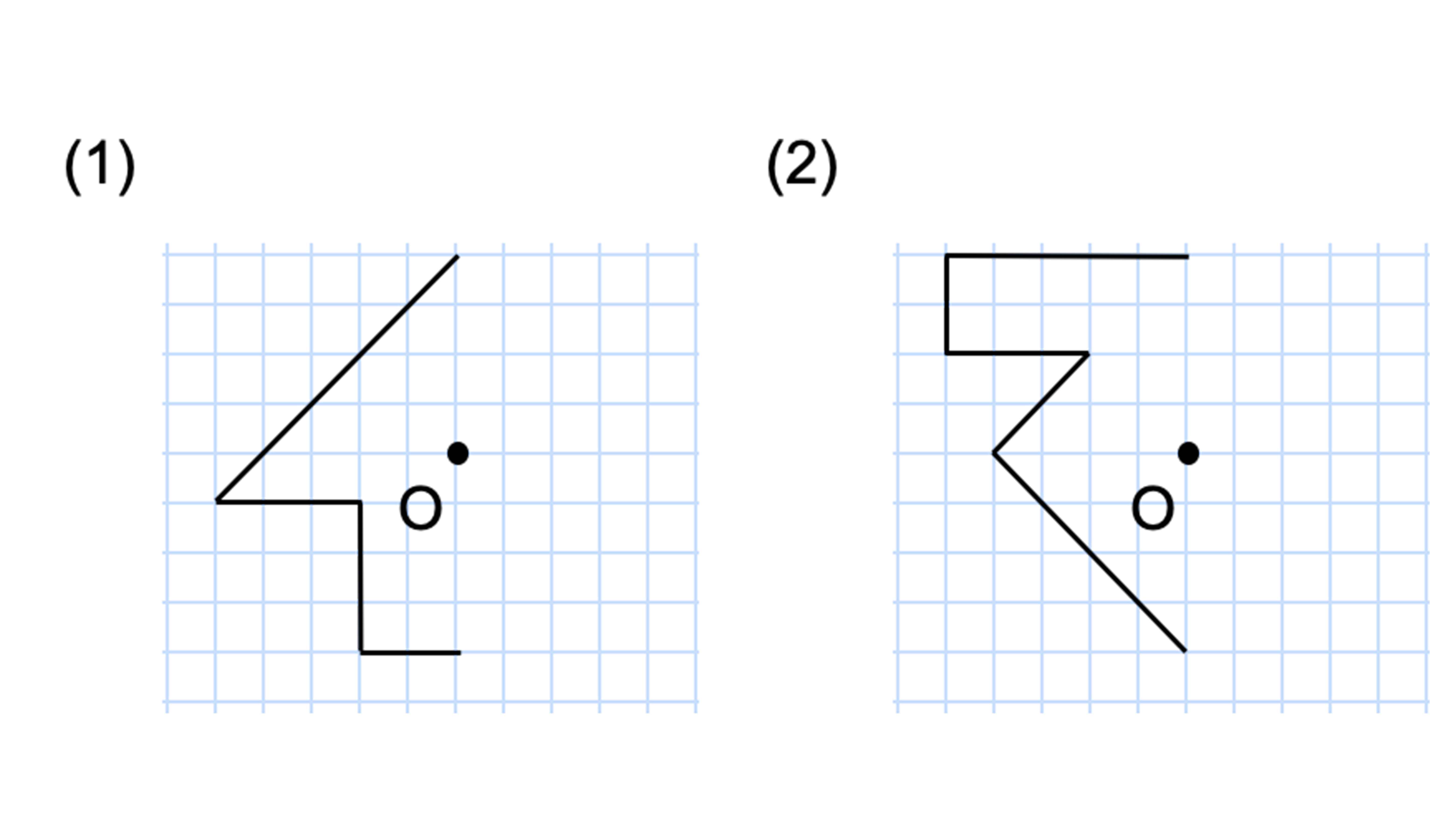
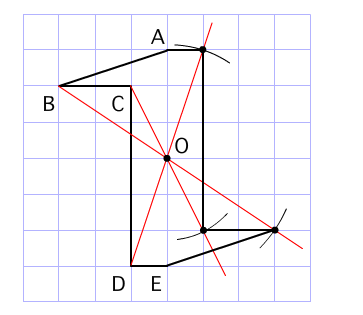
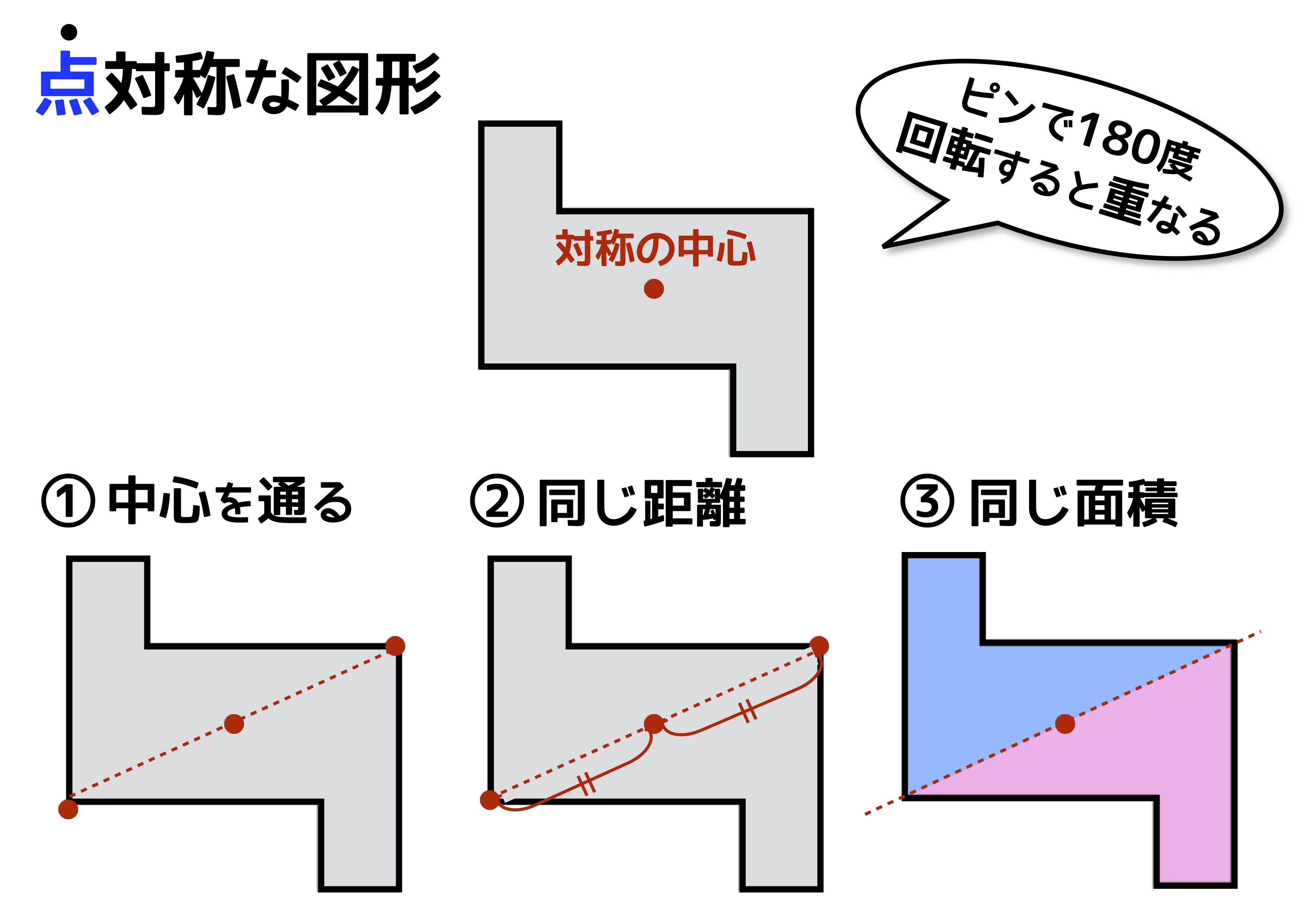
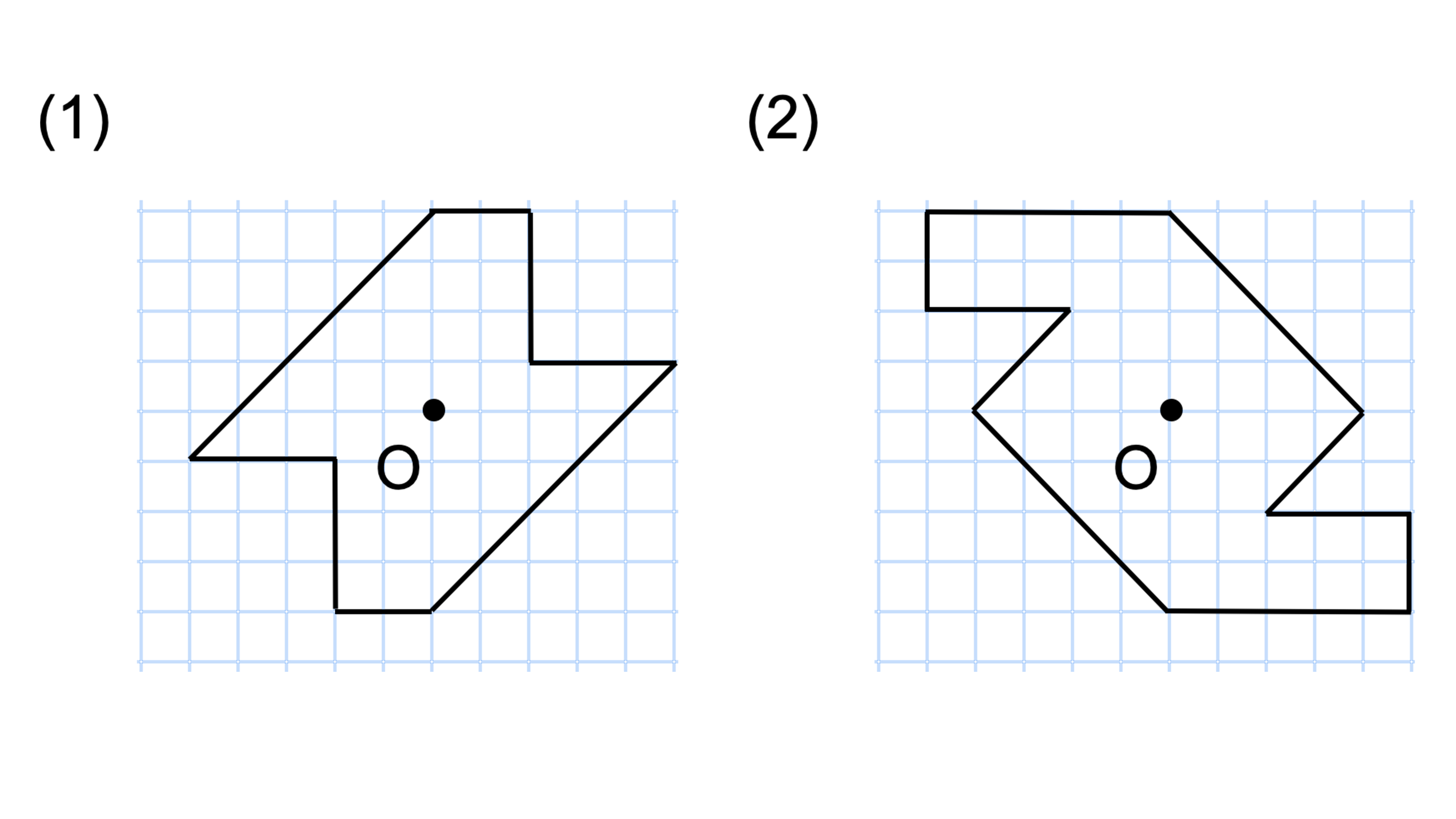
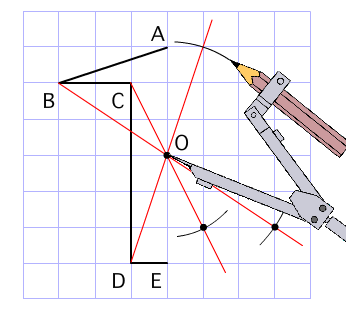
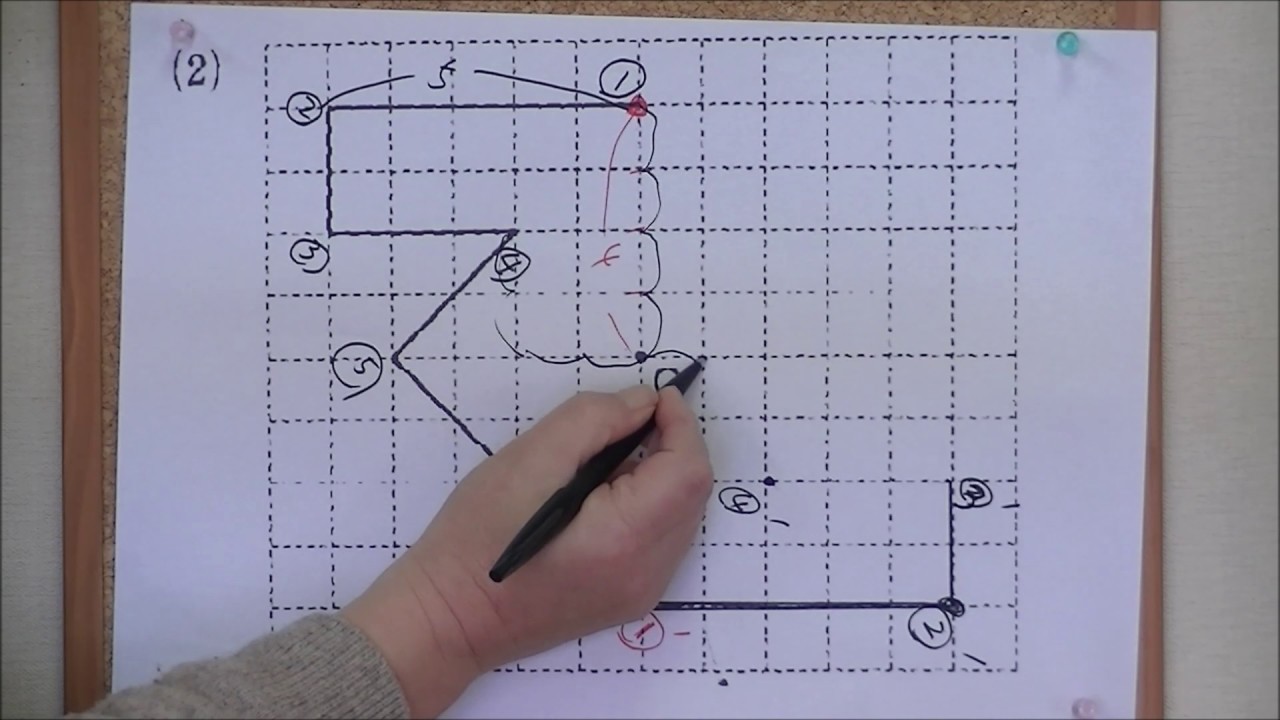
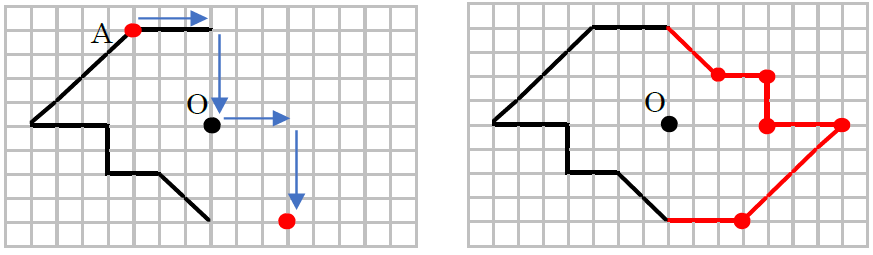
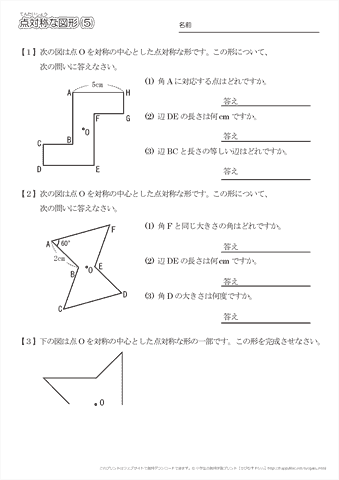
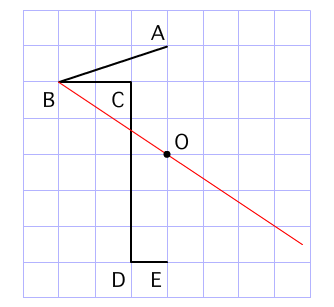
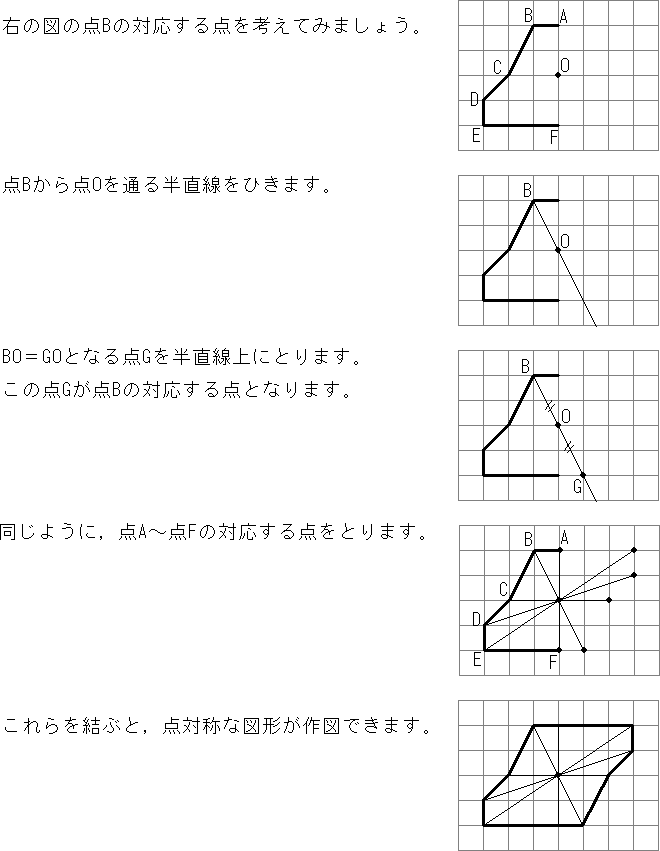
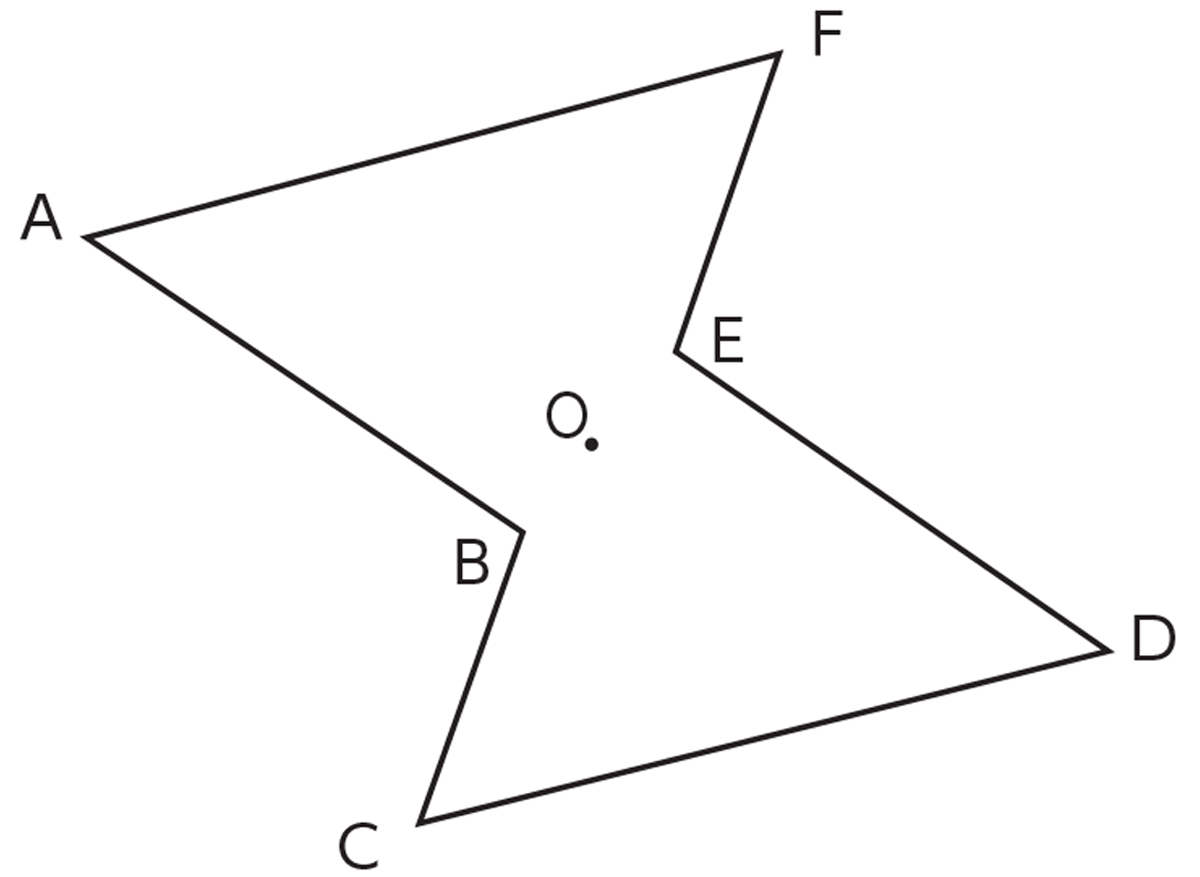
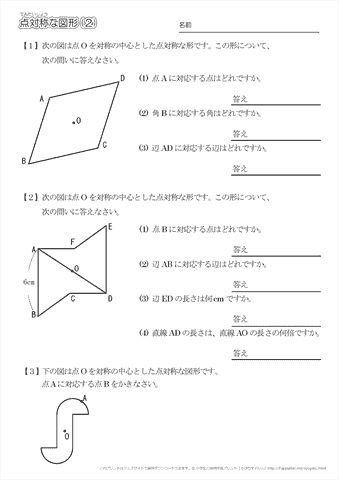
このとき、2つの対角線を結んで交わった点が 対称の中心 です。 点対称な図形では、対称の中心のまわりに180°回転させたときに重なり合う点、辺、角のことをそれぞれ、 「対応する点」「対応する辺」「対応する角」 といいます。 線対称のときと同じ この線対称と点対称自体をお子さんに教えるにも、「線対称=ある直線を折り何かと教えづらい「線対称・点対称①」(小6) このように、先に図形の頂点を対称に書きます。 また、このブログでの点対称、線対称の考え方は高校生でも通用できる考え 6年算数「対称な図形」指導実践 点対称のかき方のコツ 点対称を作図するのは難しい 下のような図に、点Oを中心に点対称をかくとします。 まずは、ポイントとなるかどに印をつけます。 「かどをえんぴつでぐりぐりしなさ〜い」 次に、そのぐりぐりに
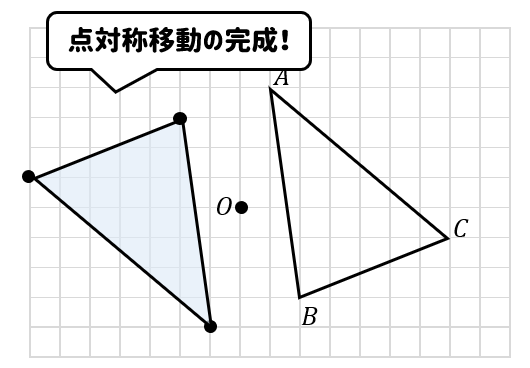
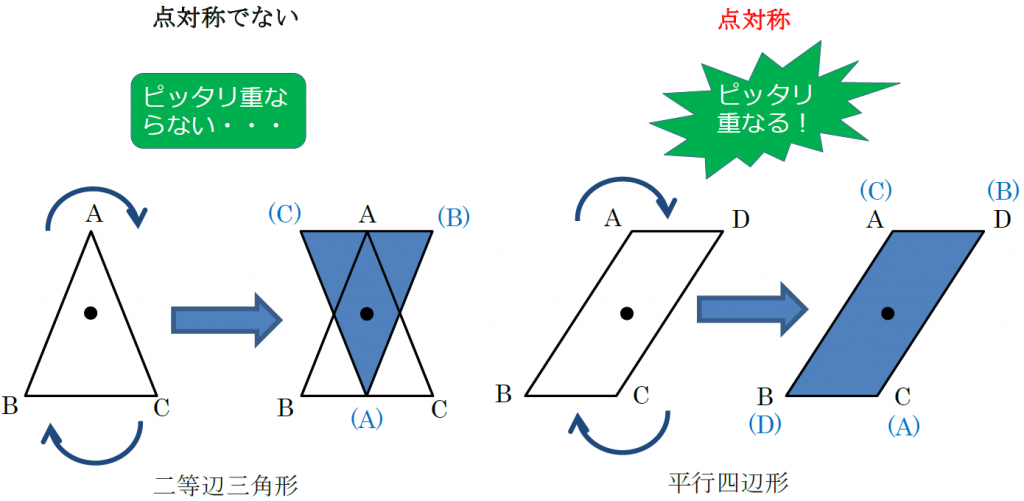
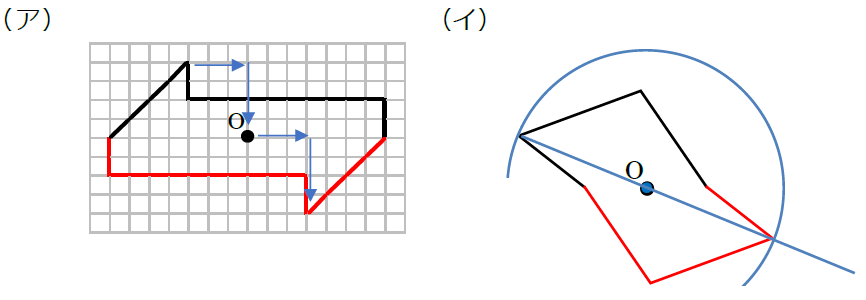
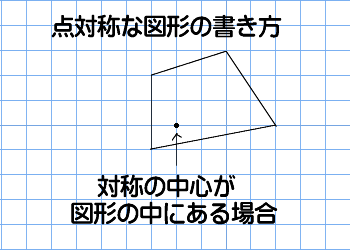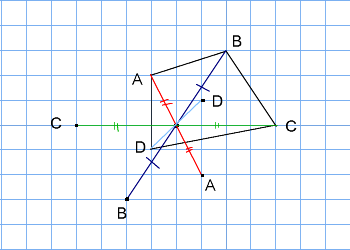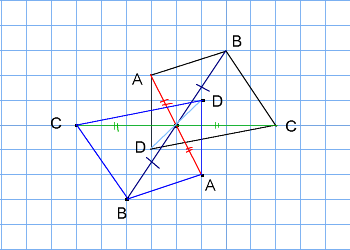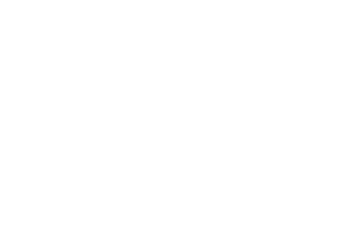
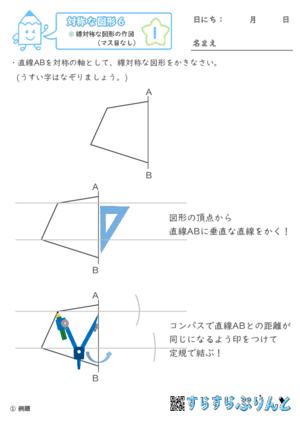
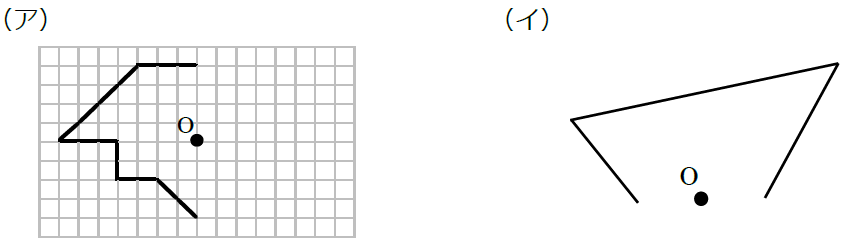
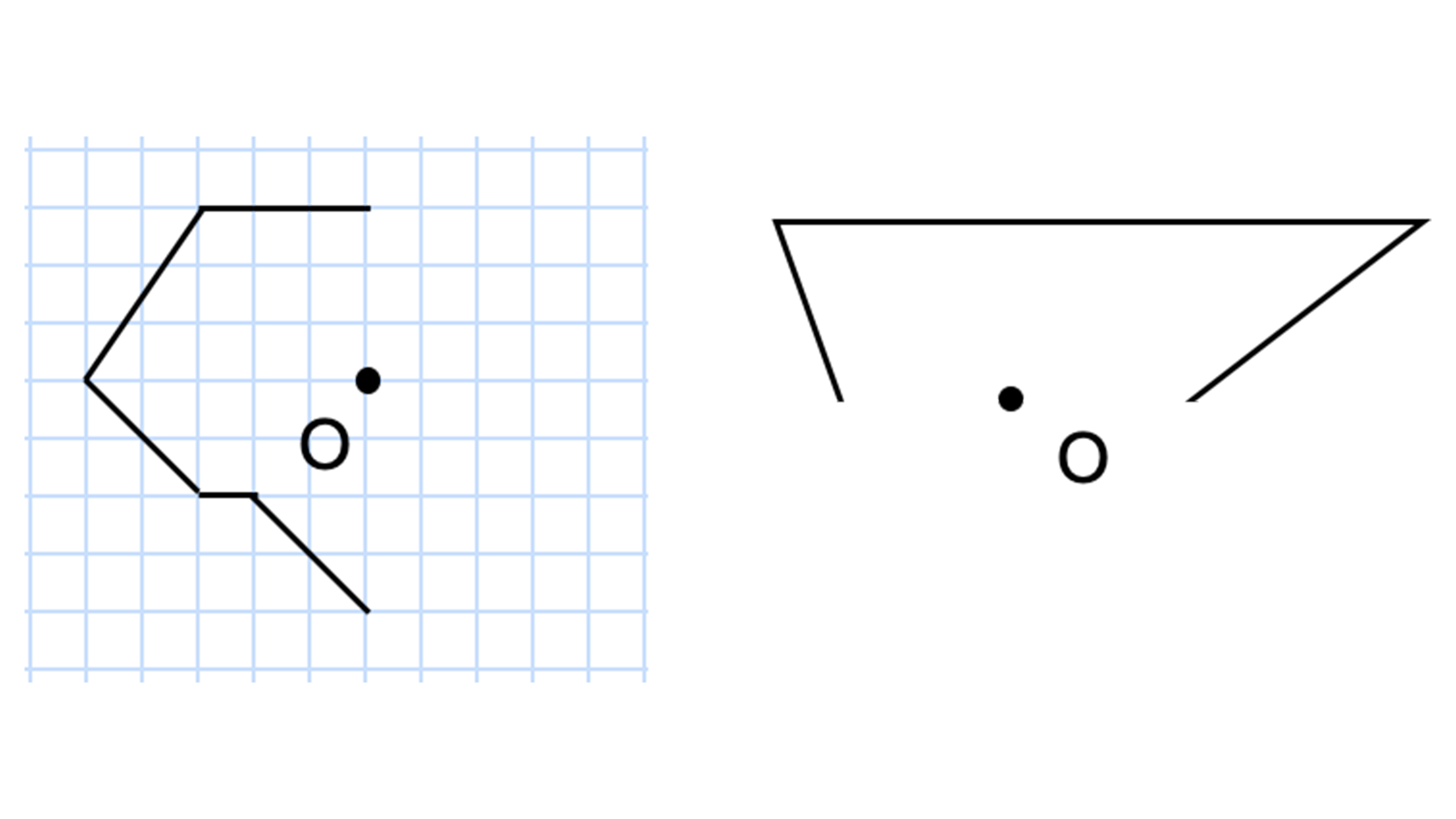
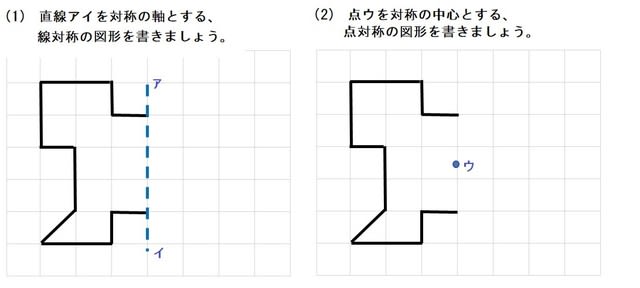
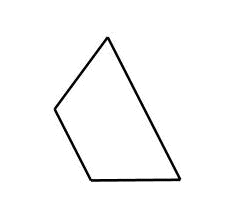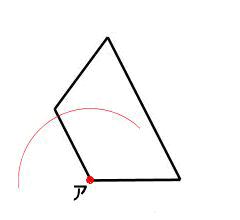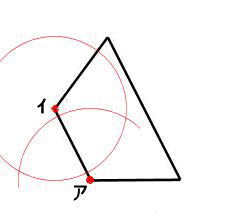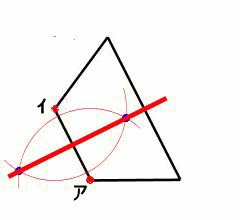
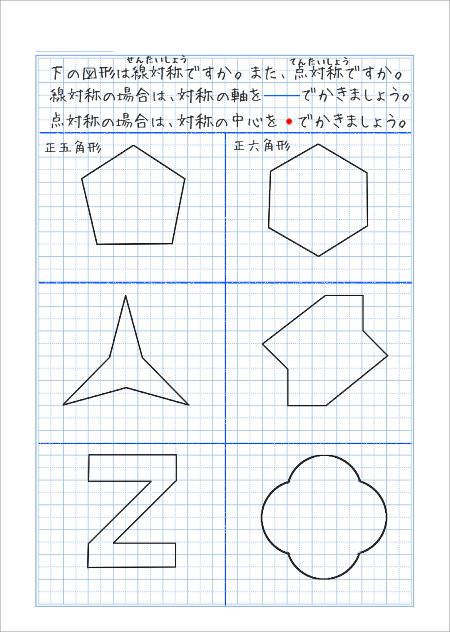
図形があります ここでは、 「線対称(せんたいしょう)な図形」 「点対称(てんたいしょう)な図形」 という、2つのグループの図形について見ていきましょう こちらの図形を見てください 左の辺と右の辺の長さが等しい 「二等辺三角形」ですね 点対称な図形の書き方 点対称な図形の書き方は、対称の中心と対応する点を直線で結ぶことがポイントとなります。 各頂点から点Oを通る直線を書きます。 そして点Oから頂点と同じな長さになるところに点をとります。 点を結んで完成です。 マス目が 左が線対称、右が点対称です。 上の図にならって性質を書き変えると下のようになります。 先ほどのような文章で覚えるよりもこちらの方が短くて覚えやすいのではないでしょうか。 点対称 AB上に点Oがある ← (点対称の性質1) AO=BO ← (点対称の性質2) 線対称の性質 AC⊥アイ ← (線対称の性質1) AO=CO ← (線対称の性質2) そして線対称と点対称の図形を見分ける問題は
点 対称 書き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 | ||
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 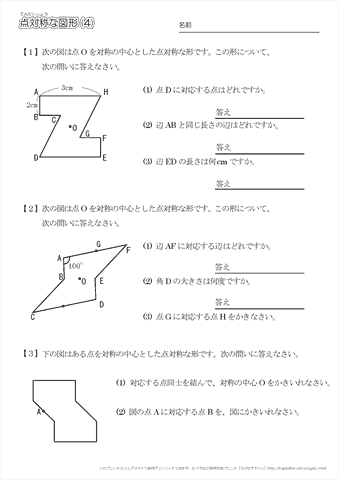 | 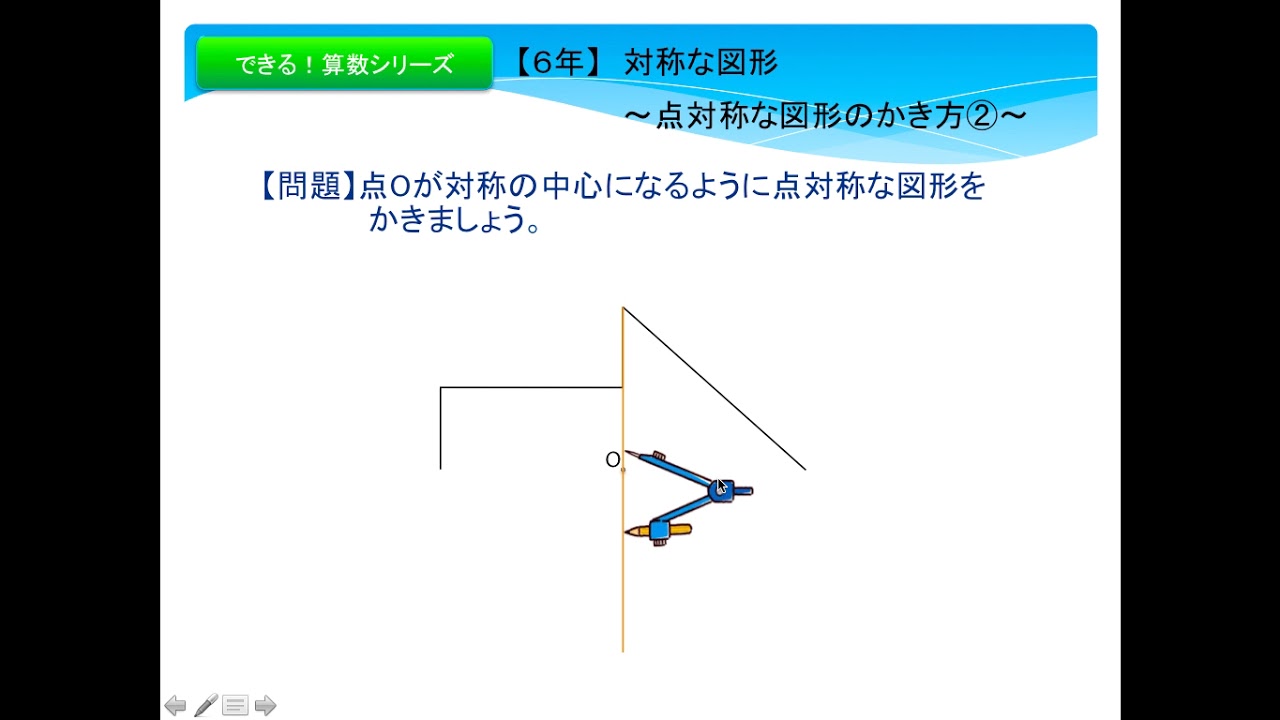 |
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
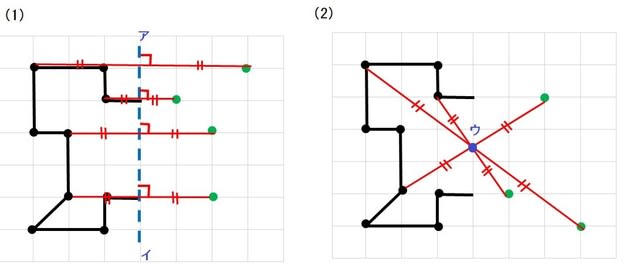 |  | |
 |  | |
 |  | |
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「点 対称 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
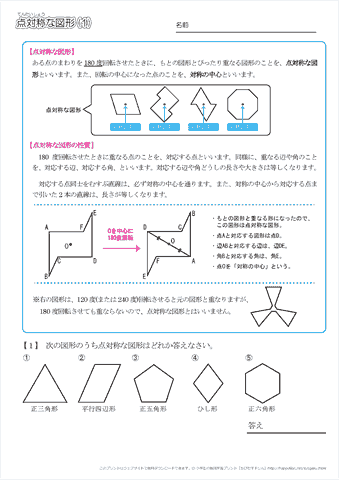
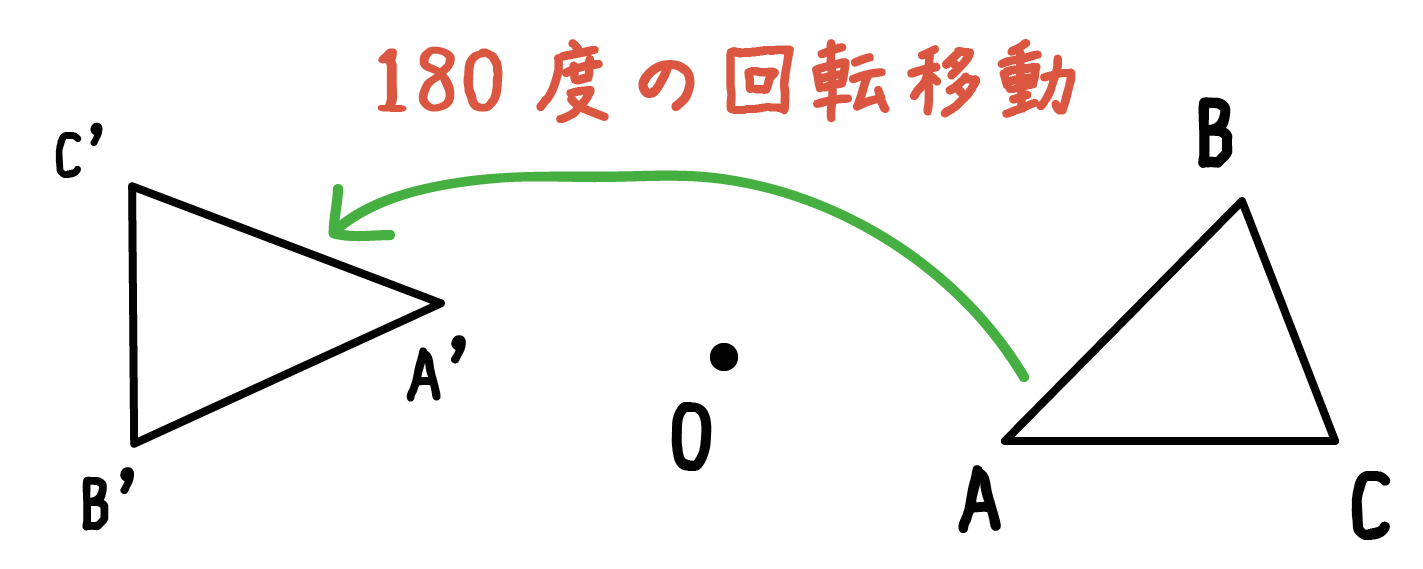
対称な図形 点対称基本1 無料で使える学習ドリル manabixsrvjp 1 次の にあてはまる言葉を書きましょう。 図 A 図 B 上の左の図(図A) を点Oを中心に180度回転させると 右の図のような図形(図B)ができます。 Bのような図形を な図形といいます。点対称(てんたいしょう、 point symmetry, point reflection )とは、対称性の一種である。点対称な図形は、対称点(対称中心)を中心とした反転に対し不変である。また、そのような図形を、点対称な図形という。 対称点 点対称操作では、1点のみが不動点で





0 件のコメント:
コメントを投稿